数独を解く

「数独」と呼ばれるパズルをご存知だろうか。
またの名をナンバープレイス、あるいは略してナンプレともいう。
一定のルールに従って、9×9のマス目に数字を埋めていくパズルである。

ルールはいたって簡単で、制約は「タテヨコの各列、および、全体を9分割して3×3に区切った各領域で、いずれも1から9までの数字が重複なく配置されるように数字を並べなさい」というだけのもの。
いくつかのマスにはあらかじめ初期値が与えられており、それをヒントに空いているマスを埋めていく。
制約を満たしつつ全てのマス目に数字を書き入れることができれば、それがゴールである。

いささか古い記事ではあるが、「解けたら天才！フィンランドの数学者が作った「世界一難しい数独」」と題した記事がある。
この記事で紹介されている「世界一難しい数独」とは、次のような問題だ。

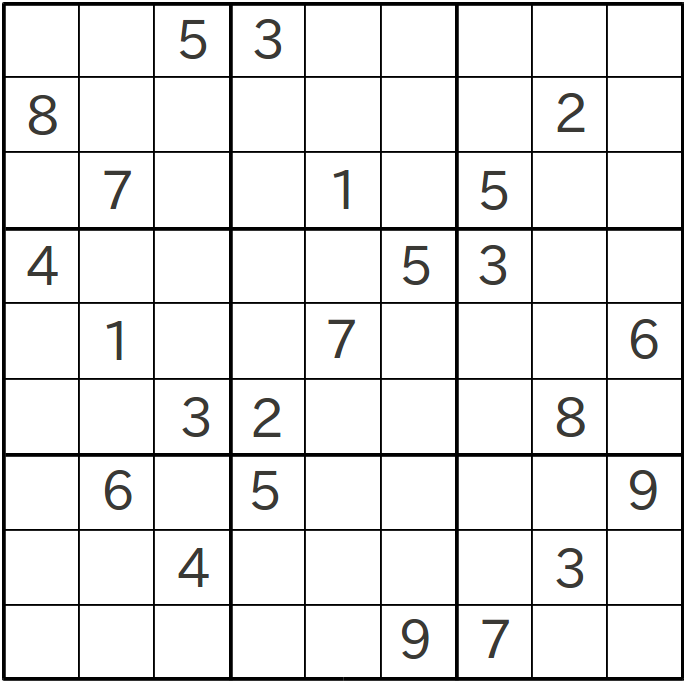
数独を解くことに関してはいささか自信があった私だが、確かにこの問題は難しく、かなりの歯ごたえを感じた。
どうやら一朝一夕には解けそうもない。
ついに、業を煮やした私は、計算機の力を借りて解くことにした。

もっとも、既存の数独を解くソフトウェアを利用するのではつまらない。
せっかくなので、解を探索するプログラムを書くところから始めてみる。

解の探索プログラム

この手の問題に対する最も単純な解き方は、力任せに解を探していく方法である。
アルゴリズムの骨子は、以下のとおり。

空いているマスを、端から順番に試していく。
まずは、途中まで問題なく進んできたとして、対象とするマスを考えてみる。
このマスに、1から9までの数字を順番に埋めて試すことを考えよう。
数字を入れて、その段階で制約を満たしているかどうか、判定する。
制約を満たしているなら、次の空いているマスに進もう。対象とするマスを1つ進めて、1から次の手順を始めよう。
制約を満たしていないときは、数字を更新して、2.に戻る。
1から9まで全て試してみて、どれもダメだったら、ここまでの手順に問題があったはず。
ここまで埋めてきたマスを1つ戻し、やり直してみる。

これは、再帰呼び出しを利用した（深さ優先）探索が適用できる問題の典型的な例だ。
再帰呼び出しの終端条件は、制約を満たしたまま、空いている最後のマスまで到達したことに相当する。

これをCふうの擬似コードで表現すると、次のように書くことができる。
なお、関数check(cell*)は、引数で取るマス目が制約を満たしているか否かを判定するための関数とする。
関数の構造を右側のコメントで示した。とても単純な構成であることが分かるだろう。


boolean solver(cell* target) {
  if (target == NULL) return TRUE; // 最後まで到達したからOK

  for (int i = 1; i <= 9; i++) {
    target->val = i;                     // i を入れてみて
    if ((check(target) == TRUE) &&       // 現段階がOKで
        (solver(target->next) == TRUE))  // その先もOKなら
       return TRUE;                      // OKを返そう
  }
  target->val = 0;           // どれもダメだったので空にして
  return FALSE;              // NGを返そう（やり直し）
}

ここで、構造体cellの定義は下記のとおり。


typedef struct _cell cell;
struct _cell {
  unsigned char val;  // マスの値
  cell* next;         // 次に空いているマスへのポインタ
};

この構造体は、マス目の値と、別の構造体cellデータへのポインタを持つ。
また、このポインタを利用して、あらかじめ次に空いているマスへのポインタを利用したリンク構造を事前の準備で実現しているものとしよう。
再帰による解の探索過程では、このリンク構造を上手に使い、空いているマスを辿っていく。
リンク構造の終端はNULL、すなわち次を指すポインタがNULLであることで、最後のマスまで到達したかどうかを判定できるというしくみだ。

前処理や制約の判定処理まで含め、Cで記述したコードを本稿の末尾に示しておく。
クイック・ハックで書いたコードなので、多少の改善を加える余地、リファクタリングすべきコードがまだ残されている点には目をつぶって頂きたい。
本プログラム、解を探索するアルゴリズム部分の記述は全体の1割に満たない。
データ構造をうまく構築することで、すっきりと記述できることを確認できるだろう。

様々なアプローチによる数独ソルバー

世の中にはいろいろなことを考える人がいるもので、SQLで数独を解くという解説もある。
確かに条件に合致した検索を得意とするSQLや、宣言型プログラミングのPrologなどは、この手のパズルを解くためのプログラミングと親和性が高いだろう。

また、本稿で紹介したブルートフォース的なアプローチではなく、人間の思考を辿るような、よりエレガントな解法による解の探求を実現しようという試みもある。
例えばこのソルバーは、いくつかの定石に従って部分的な解を求めた後で、虱潰しの探索を試みる。
本稿で試した問題を実際に試してみると、けっこうな時間がかかったのち、「超むつかしい（別解あるかも？）」というメッセージとともに正解が出た。

解の探索方法は本稿で紹介したものと同じながら、探索の過程を可視化して示してくれるツールもある。
可視化のスピードを変化させることができ、探索の手順を確認しやすくなっている。

数独だけでなく、様々なパズルをプログラミングで解くという課題は、パズルに対する搦め手からのチャレンジだ。
皆さんも、夏休みの宿題に、頭の体操として挑戦してみてはいかがだろうか。

本文中のリンク・関連リンク：

日々是遊戯：解けたら天才！フィンランドの数学者が作った「世界一難しい数独」
SQLによる数独の解法
無料数独解法プログラム/ナンプレ解く/SUDOKU SOLVER
My Shelf : ナンバープレース（数独）… このソルバーは本稿の問題を解けなかった
Sudoku Java Solver Applet by Klaas（英語）
数独を解く(画像解析) — cuspy diary：画像解析で印刷された数独パズルを解こうというお話
世界一難しい数独を解く：Microsoft Solver Foundation (MSF)を使って解こうという挑戦。本稿と同じ問題にチャレンジ

（付録）Cによる数独ソルバー


#include <stdio.h>
#include <string.h> // for memset()
#include <math.h>   // for floor()

#define FALSE 0
#define TRUE  1

typedef struct _cell cell;
typedef cell* cell_p;

struct _cell {
  unsigned char val;
  cell_p	row [9];
  cell_p	col [9];
  cell_p	area[9];

  cell_p	next;
};

cell matrix[81];

unsigned char rawdata[81] = 
  {0,0,5,3,0,0,0,0,0,
   8,0,0,0,0,0,0,2,0,
   0,7,0,0,1,0,5,0,0,
   4,0,0,0,0,5,3,0,0,
   0,1,0,0,7,0,0,0,6,
   0,0,3,2,0,0,0,8,0,
   0,6,0,5,0,0,0,0,9,
   0,0,4,0,0,0,0,3,0,
   0,0,0,0,0,9,7,0,0};

cell_p
prepare_matrix ()
{
  int x, y, i;
  cell_p target = matrix;
  for (y = 0; y < 9; y++)
    for (x = 0; x < 9; x++)
    {
      // set value
      target->val = rawdata[y*9+x];

      // set row,col
      int x0, y0, u, v;
      for (i = 0; i < 9; i++)
      {
        target->row[i] = &(matrix[i*9+x]);
        target->col[i] = &(matrix[y*9+i]);
      }

      // set area
      x0 = floor(x / 3) * 3;
      y0 = floor(y / 3) * 3;
      i = 0;
      for (v = y0; v < y0 + 3; v++)
        for (u = x0; u < x0 + 3; u++)
        {
          target->area[i] = &(matrix[v*9+u]);
          i++;
        }

      target++;
    }

  cell_p next = NULL;
  cell_p head = NULL;
  for (i = 80; i >= 0; i--)
  {
    if (rawdata[i] == 0)
    {
      head = matrix + i;
      head->next = next;
      next = head;
    }
  }

  return head;
}

void
print_matrix ()
{
  int x, y;
  for (y = 0; y < 9; y++)
  {
    for (x = 0; x < 9; x++)
      printf (" %d", matrix[y*9+x].val);
    printf ("\n");
  }   
}

int
check (cell_p target)
{
  unsigned char tmp[10];
  int i;

  memset (tmp, 0, 10);
  for (i = 0; i < 9; i++)
  {
    int val = target->row[i]->val;
    if ((val > 0) && (tmp[val] > 0)) return FALSE;
    tmp[val] = val;
  }

  memset (tmp, 0, 10);
  for (i = 0; i < 9; i++)
  {
    int val = target->col[i]->val;
    if ((val > 0) && (tmp[val] > 0)) return FALSE;
    tmp[val] = val;
  }

  memset (tmp, 0, 10);
  for (i = 0; i < 9; i++)
  {
    int val = target->area[i]->val;
    if ((val > 0) && (tmp[val] > 0)) return FALSE;
    tmp[val] = val;
  }
  return TRUE;
}

int
solver (cell_p target)
{
  if (target == NULL) return TRUE;

  int ctr;
  for (ctr = 1; ctr <= 9; ctr++)
  {
    target->val = ctr;
    if ((check (target) == TRUE) &&
        (solver (target->next) == TRUE)) return TRUE;
  }
  target->val = 0;

  return FALSE;
}

int
main (int argc, char** argv) 
{
  cell_p target = prepare_matrix ();

  printf("Problem is ... \n");
  print_matrix ();
  printf("----------\n");

  if (solver (target) == FALSE)
  {
    printf ("no answer\n");
    return -1;
  }
  print_matrix ();

  return 0;
}